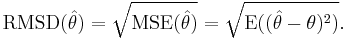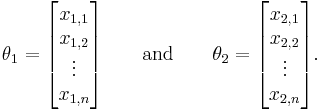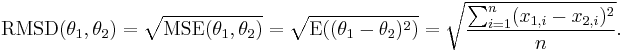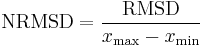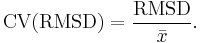Root-mean-square deviation

For the application of root mean square deviation to bioinformatics, see Root mean square deviation (bioinformatics).

The root-mean-square deviation (RMSD) or root-mean-square error (RMSE) is a frequently used measure of the differences between values predicted by a model or an estimator and the values actually observed from the thing being modeled or estimated. RMSD is a good measure of accuracy. These individual differences are also called residuals, and the RMSD serves to aggregate them into a single measure of predictive power.

1 Formula
2 Normalized root-mean-square deviation
3 CV (RMSD)
4 Applications
5 See also
6 References

Formula

The RMSD of an estimator 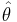$\hat{\theta}$ with respect to the estimated parameter $\theta$ is defined as the square root of the mean square error:

$\operatorname{RMSD}(\hat{\theta}) = \sqrt{\operatorname{MSE}(\hat{\theta})} = \sqrt{\operatorname{E}((\hat{\theta}-\theta)^2)}.$

For an unbiased estimator, the RMSD is the square root of the variance, known as the standard error.

In some disciplines, the RMSD is used to compare differences between two things that may vary, neither of which is accepted as the "standard". For example, when measuring the average distance between two oblong objects, expressed as random vectors

$\mathbf{\theta}_1 = \begin{bmatrix} x_{1,1} \\ x_{1,2} \\ \vdots \\ x_{1,n} \end{bmatrix} \qquad \mathrm{and} \qquad \mathbf{\theta}_2 = \begin{bmatrix} x_{2,1} \\ x_{2,2} \\ \vdots \\ x_{2,n} \end{bmatrix}.$

The formula becomes:

$\operatorname{RMSD}(\mathbf{\theta}_1, \mathbf{\theta}_2) = \sqrt{\operatorname{MSE}(\mathbf{\theta}_1, \mathbf{\theta}_2)} = \sqrt{\operatorname{E}((\mathbf{\theta}_1 - \mathbf{\theta}_2)^2)} = \sqrt{\frac{\sum_{i=1}^n (x_{1,i} - x_{2,i})^2}{n}}.$

Normalized root-mean-square deviation

The normalized root-mean-square deviation or error (NRMSD or NRMSE) is the RMSD divided by the range of observed values, or:

$\mathrm{NRMSD} = \frac{\mathrm{RMSD}}{x_\max -x_\min}$

the value is often expressed as a percentage, where lower values indicate less residual variance.

CV (RMSD)

The coefficient of variation of the RMSD, CV(RMSD), or more commonly CV(RMSE), is defined as the RMSD normalized to the mean of the observed values:

$\mathrm{CV(RMSD)} = \frac {\mathrm{RMSD}}{\bar x}.$

It is the same concept as the coefficient of variation except that RMSD replaces the standard deviation.

Applications

In meteorology, to see how effectively a mathematical model predicts the behavior of the atmosphere
In bioinformatics, the RMSD is the measure of the average distance between the atoms of superimposed proteins.
In Structure based drug designing, the RMSD is a measure of the difference between a crystal conformation of the ligand conformation and a docking prediction.
In economics, the RMSD is used to determine whether an economic model fits economic indicators.
In experimental psychology, the RMSD is used to assess how well models of perception explain the abilities of the human senses.
In GIS, the RMSD is one measure used to assess the accuracy of spatial analysis and remote sensing.
In hydrogeology, RMSD and NRMSD are used to evaluate the calibration of a groundwater model.^[1]
In imaging science, the RMSD is part of the peak signal-to-noise ratio, a measure used to assess how well a method to reconstruct an image performs relative to the original image.
In computational neuroscience, the RMSD is used to assess how well a system learns a given model.^[2]
In Protein nuclear magnetic resonance spectroscopy, the RMSD is used as a measure to estimate the quality of the obtained bundle of structures.
Submissions for the Netflix Prize are judged using the RMSD from the test dataset's undisclosed "true" values.
In simulation of energy consumption of buildings, the RMSE and CV(RMSE) are used to calibrate models to measured building performance.

References

^ Anderson, M.P.; Woessner, W.W. (1992). Applied Groundwater Modeling: Simulation of Flow and Advective Transport (2nd Edition ed.). Academic Press.
^ Ensemble Neural Network Model